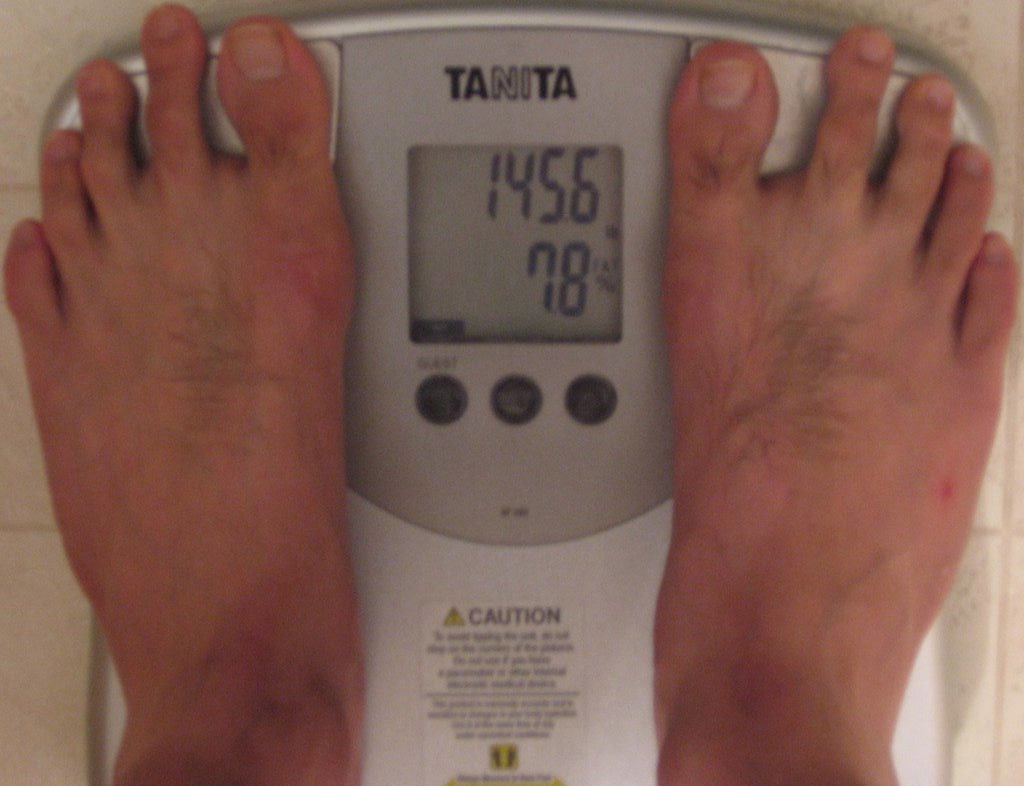
145.6 lbs (66.2 kg).
7.8% body fat.
At 6 feet 2 inches (187 cm), the numbers may seem really skinny by normal standards, but, in the cycling world, it is actually the average for billy goats. I.e. climbers.
For the time being, 7.5% to 8% body fat is my comfortable level. At 7% body fat and below, I feel cold easily.
How important is weight?
What makes a great climber, especially in the mountains, is an excellent power to weight ratio.
Power to weight ratio has two components: first, the ability to ride for long periods of time at a Maximum Sustainable (MS) power.
Typically a top climber can ride at 10% or more above threshold power (or threshold heart rate) for 30-60 minutes.
Second, top climbers have a low enough body weight so that the MS power translates into an advantage going uphill. Having a high maximum sustainable power output will make an excellent time-trialist on flat roads where the main obstacle is wind drag.
To carry over this advantage to climbing, you need a low enough body weight in relation to your MS power. This is especially true on long and steep climbs.
On short climbs of less than 5 minutes, so-called "non-climbers" can still make it over with the front riders with their very high MS power even though they may have an inferior power-to-weight ratio, due to their heavier body weight.
Bjarne Riis, winner of the 1996 Tour de France, illustrated how much body weight can make a difference while going uphill. Riis beat the great Miguel Indurain in 1996. At the time of his win Riis weighed 150lbs (68kgs) and had a MS power of 480 watts while going all-out on a climb or time trial. This gave him an incredible power to weight ratio of 7 watts per kilogram (480 / 68 = 7). 7 watts /kg is widely regarded as the magic number in order to be one of the world's best.
Indurain had a MS power of 550 watts when going all-out, a much higher number than Riis. However, he weighed in at 176lbs (80kgs), 26lbs heavier than Riis! This gave him a power to weight ration of 6.8 watts/kg (550 / 80 = 6.8), 0.2 less than Riis.
Indurain's much higher MS power gave him the advantage in the time trials, where the main obstacle is wind drag. However, on the longest, steepest climbs of the Tour, this was not the case, as Riis' 0.2 watts/kg advantage made all the difference.
[ . . . ]
Some cyclists are already at 4% - 5% body fat (for men), and in this case the only improvements they can make to their climbing is by increasing their threshold and MS power. (Source).
Here's a mathematical example:
Utilization of a rider’s Power-to-Weight Ratio (P/W) is most commonly found when assessing their climbing ability. Let us assume there are two riders of equivalent abilities with identical bikes and components. Both cyclists will be climbing the same climb side-by-side at exactly the same time on exactly the same day under exactly the same conditions.
Rider-1 weighs in at 175 lbs. and has an average sustainable power on said climb of 475 watts. Rider-2 weighs in at 130 lbs. and has an average sustainable power on the same climb of 380 watts. If someone were to base their opinion of each rider’s climbing ability solely on their power, they might think that Rider-1 would be able to easily beat Rider-2 to the top of the mountain. Granted, Rider-1’s sustainable climbing power is 95 watts GREATER THAN Rider-2’s (ca. 20%); however, power is not the only variable riders are aware of while dragging themselves up a climb. TOTAL Weight (body, bike frame, components, wheels, etc.) also plays an important role.

The effort a climbing rider (measured in power) is directed in part along each of these two vectors. Although the rider’s mass factors into each of these directional vectors, it plays a bigger role as WEIGHT when you factor in the affect of gravity along the vertical vector. Stated simply, P/W could also represent H/V as a means of determining how much of a rider’s climbing power will be used to move along the horizontal vector (general direction of progression) compared to overcoming the influences of gravity along the vertical vector.
Getting back to our two riders. When we now account for each of their weights in addition to their climbing powers, we find that P/W1 = 2.71 Watts/lb, whereas P/W2 = 2.92 Watts/lb. All things being equal, Rider-2 will get to the top of the climb before Rider-1, even though Rider-1 can generate approximately 20% more power than Rider-2. (Source)
Power-to-Weight Ratio (besides talent and physical fitness, of course) could explain for Discovery Channel Pro Cycling Team 2006's latest sign up: Janez Brajkovic.

Janez is 5 feet 8 inches (172 cm) tall, weighs between 115 to 130 lbs (52 to 59 kg), and climbs like a bat out of hell.

Since his first racing season in 2001, Brajkovic has exhibited his skill at the top U23 level and had a breakthrough season in 2004, capped by his victory at the Worlds in Italy. On paper, Holland´s Thomas Dekker appeared unbeatable, but Brajkovic won the near 37km event by 18 seconds over Dekker at an average speed of 47.0km/h (29.2mph), and was the only man to break the 47 minute mark too.
Yes, cyclists who specialize in climbing look scrawny, but try keeping up with them in the mountains.
Any hulk, wrestler, or macho man who thinks otherwise is welcome to prove me wrong by joining me for a Mount Hamilton Double with 9536 ft / 2907 m of climbing (road), or a Mount Diablo Double with 9044 ft / 2757 m of climbing (off-road). Let's see how your giant pecs and 400 lb (181 kg) bench presses help you keep up in the mountains :P

No comments:
Post a Comment